Details
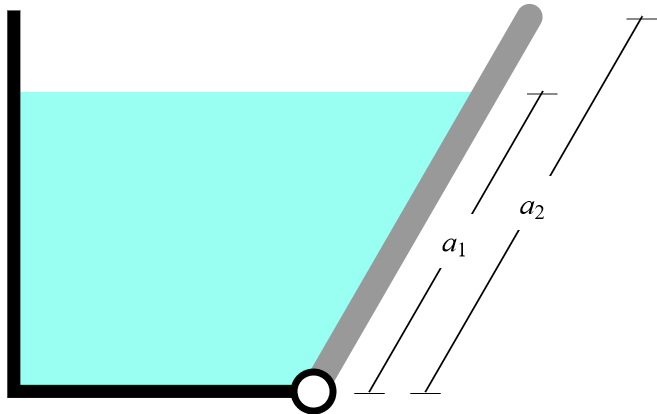
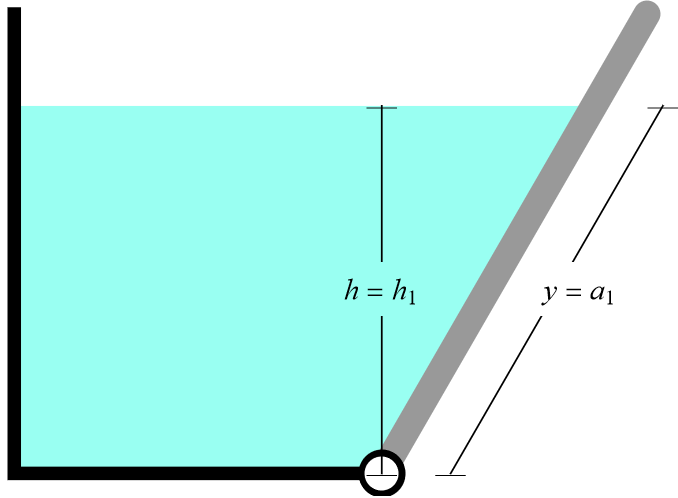
This simulation determines the cable tension necessary to support a gate partially submerged under water. The gate is \( a_{2} \) meters long, and the distance from the hinge to top of the water along the gate is \( a_{1} \) meters. The vertical distance down from the top of the liquid is \( h \), and \( y \) is the distance along the gate, starting from the water's surface, such that \( h = h_{1} \) at the bottom of the container, and \( y = a_{1} \) at the hinge:
 The magnitude of the resultant force due to the water is found by summing the differential forces \( dF = \gamma \, h \, dA \) over the entire surface:
$$
[1] \quad F_{R} = \int_{A} \gamma \, h \, dA = \int_{A} \, \gamma \, y \, \mathrm{sin ( \theta )} \, dA
$$
where \( F_{R} \) is the resultant force (N), \( \gamma \) is the specific weight of water (9.807 kN/m3), \( h = y \, \mathrm{ sin ( \theta ) } \) is the vertical distance from the top of the water to any point in the water (m), \( \theta \) is the angle of the gate (degrees), \( dA = b \, dy \) is differential area of the gate (m2), and \( b \) is the width of the gate (m). Note that the specific weight \( \gamma \) is the specific gravity \( \rho \) times the acceleration of gravity \( g \). The total area of the gate that is in contact with water is \( A_{gate} = b \, a_{1} \). This integral is from \( y = 0 \) at the top of the water level to \( y = a_{1} \) at the hinge. Since \( \gamma \) is constant, and for a fixed value of \( \theta \), the resultant force becomes:
$$
[2] \quad F_{R} = \gamma \, \mathrm{sin(\theta)} \int_{A} y \, dA
$$
The integral \( \int_{A} y \, dA \) is:
The magnitude of the resultant force due to the water is found by summing the differential forces \( dF = \gamma \, h \, dA \) over the entire surface:
$$
[1] \quad F_{R} = \int_{A} \gamma \, h \, dA = \int_{A} \, \gamma \, y \, \mathrm{sin ( \theta )} \, dA
$$
where \( F_{R} \) is the resultant force (N), \( \gamma \) is the specific weight of water (9.807 kN/m3), \( h = y \, \mathrm{ sin ( \theta ) } \) is the vertical distance from the top of the water to any point in the water (m), \( \theta \) is the angle of the gate (degrees), \( dA = b \, dy \) is differential area of the gate (m2), and \( b \) is the width of the gate (m). Note that the specific weight \( \gamma \) is the specific gravity \( \rho \) times the acceleration of gravity \( g \). The total area of the gate that is in contact with water is \( A_{gate} = b \, a_{1} \). This integral is from \( y = 0 \) at the top of the water level to \( y = a_{1} \) at the hinge. Since \( \gamma \) is constant, and for a fixed value of \( \theta \), the resultant force becomes:
$$
[2] \quad F_{R} = \gamma \, \mathrm{sin(\theta)} \int_{A} y \, dA
$$
The integral \( \int_{A} y \, dA \) is:
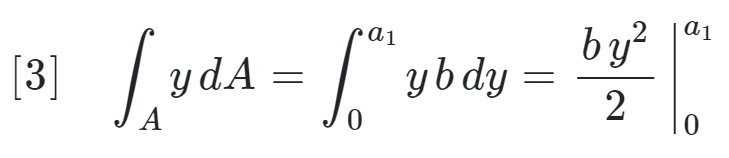 this is then equal to:
$$
[4] \quad \int_{A} y \, dA = \frac{b}{2} a^{2}_{1} = A_{gate} \frac{a_{1}}{2}
$$
the resultant force is then:
$$
[5] \quad F_{R} = \gamma \, \mathrm{sin( \theta )} A_{gate} \frac{a_{1}}{2}
$$
The sum of the moments around the hinge is equal to the moment of the resultant force at the y coordinate \( y_{R} \). Note that moment is proportional to the distance from the hinge to location of the force:
$$
[6] \quad F_{R} ( a_{1} - y_{R} ) = \int_{A} \gamma \, y \, (a_{1} - y) \, \mathrm{sin(\theta)} \, dA = \gamma \, \mathrm{sin(\theta)} \int_{0}^{a_{1}} y \, (a_{1} - y) \, b \, dy
$$
this is then equal to:
$$
[4] \quad \int_{A} y \, dA = \frac{b}{2} a^{2}_{1} = A_{gate} \frac{a_{1}}{2}
$$
the resultant force is then:
$$
[5] \quad F_{R} = \gamma \, \mathrm{sin( \theta )} A_{gate} \frac{a_{1}}{2}
$$
The sum of the moments around the hinge is equal to the moment of the resultant force at the y coordinate \( y_{R} \). Note that moment is proportional to the distance from the hinge to location of the force:
$$
[6] \quad F_{R} ( a_{1} - y_{R} ) = \int_{A} \gamma \, y \, (a_{1} - y) \, \mathrm{sin(\theta)} \, dA = \gamma \, \mathrm{sin(\theta)} \int_{0}^{a_{1}} y \, (a_{1} - y) \, b \, dy
$$
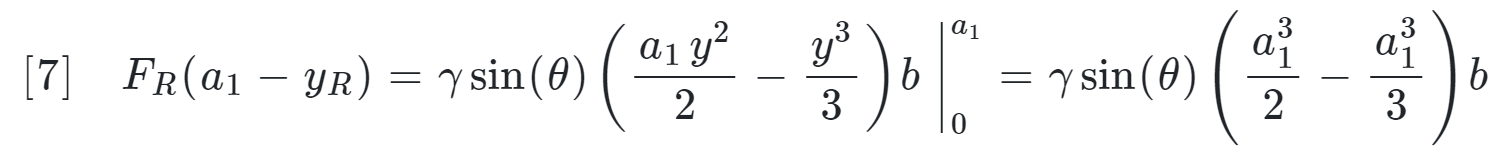 therefore,
$$
[8] \quad F_{R} ( a_{1} - y_{R} ) = \gamma \, \mathrm{sin(\theta)} \frac{a_{1}^{2}}{6} A_{gate}
$$
and substituting equation [5] into equation [8] and simplifying:
$$
[9] \quad y_{R} = \frac{ 2 \, a_{1} }{ 3 }
$$
That is, the resultant force is located 1/3 of the distance from the hinge to the water level along the gate (because \( y_{R} \) is the distance of the moment along the gate starting from the water's surface). A moment balance determines the tension \( T \) (kN) of the cable that is holding up the gate:
$$
[10] \quad \sum M_{i} = 0 = F_{R} \frac{a_{1}}{3} + W_{gate} \frac{a_{2}}{2} \mathrm{cos(\theta)} - T \, a_{2} \, \mathrm{sin(\theta)}
$$
where \( M_{i} \) is moment \( i \) and \( W_{gate} \) is the weight of the gate, which has its moment located at the center of the gate. The tension is then:
$$
[11] \quad T = \frac{ F_{R} \frac{ a_{1} }{ 3 } + W_{gate} \frac{ a_{2} }{ 2 } \mathrm{cos(\theta)} }{ a_{2} \, \mathrm{sin(\theta)} }
$$
therefore,
$$
[8] \quad F_{R} ( a_{1} - y_{R} ) = \gamma \, \mathrm{sin(\theta)} \frac{a_{1}^{2}}{6} A_{gate}
$$
and substituting equation [5] into equation [8] and simplifying:
$$
[9] \quad y_{R} = \frac{ 2 \, a_{1} }{ 3 }
$$
That is, the resultant force is located 1/3 of the distance from the hinge to the water level along the gate (because \( y_{R} \) is the distance of the moment along the gate starting from the water's surface). A moment balance determines the tension \( T \) (kN) of the cable that is holding up the gate:
$$
[10] \quad \sum M_{i} = 0 = F_{R} \frac{a_{1}}{3} + W_{gate} \frac{a_{2}}{2} \mathrm{cos(\theta)} - T \, a_{2} \, \mathrm{sin(\theta)}
$$
where \( M_{i} \) is moment \( i \) and \( W_{gate} \) is the weight of the gate, which has its moment located at the center of the gate. The tension is then:
$$
[11] \quad T = \frac{ F_{R} \frac{ a_{1} }{ 3 } + W_{gate} \frac{ a_{2} }{ 2 } \mathrm{cos(\theta)} }{ a_{2} \, \mathrm{sin(\theta)} }
$$
Figure 1

Figure 2
