Forces on a Completely Submerged Gate

A gate hinged at the top is submerged under water. The gate is 2.5 meters long and 1 meter wide. This simulation calculates the force that must be applied to keep the gate closed. Use the sliders to set the water height and the gate weight. Check the "show distances" box to display distances.

This simulation determines the magnitude of the applied force needed to keep a gate, which is $ w_{2} $ meters wide and $ h_{1} $ meters tall, closed (see Figure 1 below). The magnitude of the resultant force is found by summing the differential forces over the gate surface: $$ [1] \quad F_{R} = \int_{A} \gamma \, h \, dA = \int_{A} \gamma \, y \, \mathrm{sin} ( \theta ) dA $$ where $ h = y \, \mathrm{sin} ( \theta ) $ is the vertical distance from the water surface (m), $ y $ is the y-coordinate (along the diagonal) from the water surface (m), $ F_{R} $ is the resultant force (N), $ A = L \, b $ is the gate area (m²), $ b $ is the width of the gate (m), $ L $ is the length of the gate (m) as shown in Figure 1 below, $ \theta $ is the angle (degrees) and $ \gamma $ is the specific weight of water (N/m³). Solving the integral for $ F_{R} $: $$ [2] \quad F_{R} = \gamma \, h_{c} \, A = \gamma \, y_{c} \, \mathrm{sin} (\theta) A $$ where $ h_{c} = y_{c} \, \mathrm{sin} (\theta) $ is the vertical distance from the fluid surface to the centroid of the gate (m) and $ y_{c} = D + L/2 $ is the y-coordinate of the gate centroid (m). The y-coordinate $ y_{R} $ of the resultant force can be found by summing moments around the hinge: $$ [3] \quad F_{R} (y_{R} - D) = \int_{A} (y - D) dF = \int_{A} \gamma \, y (y - D) \mathrm{sin}(\theta) dA $$ When $ F_{R} $ is substituted into this equation, and the right side is integrated from $ D $ to $ D + L $, then $ y_{R} $ becomes: $$ [4] \quad y_{R} = D + \frac{(D + L)^{2} (2L - D) + D^{3}}{6 L \, y_{c}} $$ A moment balance is done to determine the applied force that keeps the gate closed: $$ [5] \quad \sum M = 0 = -F_{R} ( y_{R} - D ) + W (y_{c} - D) \mathrm{cos} (\theta) + F_{A} \, L $$ rearranging to solve for $ F_{A} $: $$ [6] \quad F_{A} = \frac{F_{R} (y_{R} - D) - W (y_{c} - D) \mathrm{cos} (\theta)}{L} $$ where $ W $ is the weight of the gate (N), $ D $ is the diagonal length from the hinge to the top of the water (m) and $ F_{A} $ is the applied force (N).

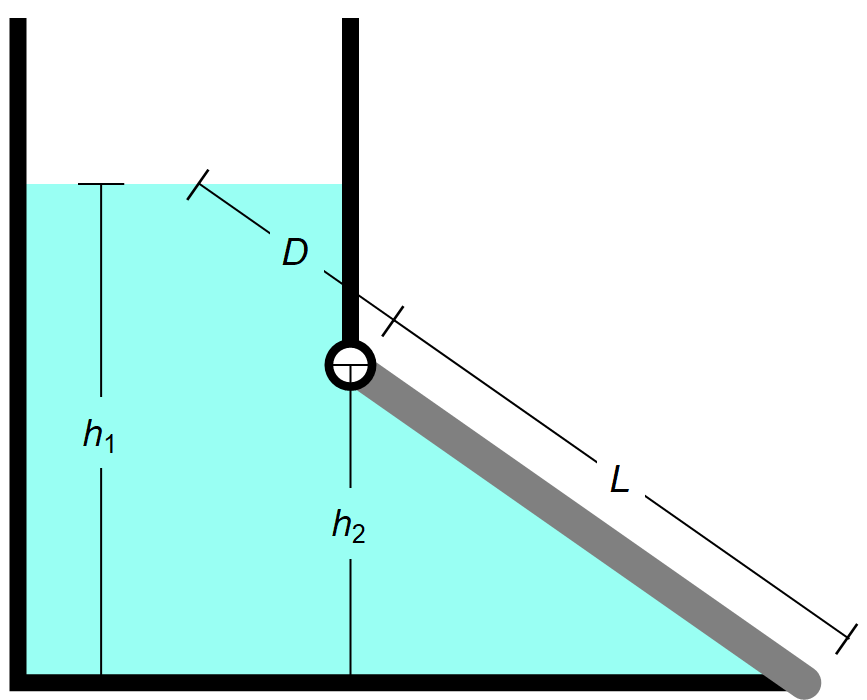
Figure 1

References:

- B. R. Munson, D. F. Young, T. H. Okiishi and W. W. Huebsch, Fundamentals of Fluid Mechanics, 6th ed., Hoboken, NJ: John Wiley and Sons, 2009 pp. 58-60

Related simulation:

- Forces on a Partially Submerged Gate