The Carnot cycle for an ideal gas is shown on a pressure-volume diagram or on a temperature-entropy diagram, chosen with the buttons. The cycle consists of two reversible isothermal steps and two reversible adiabatic steps. The temperatures of the hot and cold reservoirs (T_H and T_C, respectively) are set with sliders. The largest volume (V₂) and the smallest volume (V₁) are set with sliders, as is the heat capacity ratio (C_p/C_v) for the ideal gas. Use the buttons to switch the cycle between heat engine and heat pump configurations. The diagram on the right shows the values for heat transfer per mol; the signs of these values are for the cycle as the system. For the heat engine, \(\eta\) is the efficiency. For the heat pump, COP is the coefficient of performance.

This simulation was created in the Department of Chemical and Biological Engineering at University of Colorado Boulder for LearnChemE.com by Patrick Doyle. This simulation was prepared with financial support from the National Science Foundation. It is based on a Mathematica simulation on the Wolfram Demonstration Project website prepared by S. M. Blinder (Carnot Cycle on Ideal Gas). Address any questions or comments to learncheme@gmail.com. All of our simulations are open source, and are available on our LearnChemE Github repository.

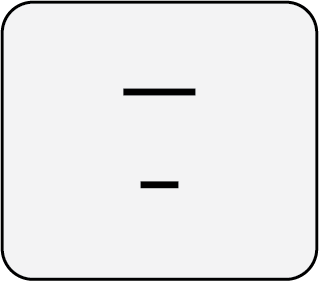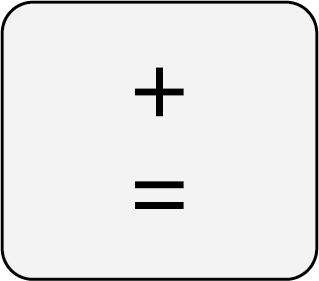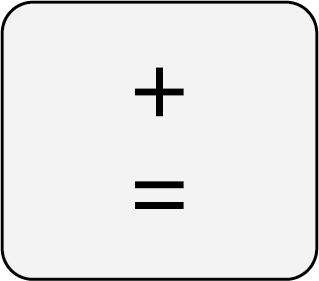If this simulation is too big for your screen, zoom out using  +  on Mac or  +  on Windows. To zoom in, use  +  on Mac or  +  on Windows.